The color bit depth of an image, is the number of bits allocated to represent each primary value (red, green and blue) of a pixel of that image. Since we are talking about digital information, each value can be coded using different Word length. These days, the typical lengths are 8, 10, 12 or even 16 bits.
An 8bit RGB pixel value would look like this: 01101001 11001010 11110010 (I added the space for reading convenience). So each pixel data of a color image is 8-3= 24bit long.
A 16bit-coded pixel would look like this: 1100110100100110 1110010100110101 1111001001100110. In this case, each pixel data is (16-3=) 48 bit long.
So a 16bit color depth image is twice the size of an 8bit one (at the same resolution). This is, of course, without considering the extra bits used for checksum, the header, eventual metadata…
In term of color resolution (I hate this term as it can be confused with image resolution), an 8bit file can represent 2^8 different levels of intensity for each primary color (red, green or blue). So, the number of different colors a pixel can display is (2^8)^3 = 16,777,216.
See the end of this article for a quick digital terms and concept glossary.
Lack of Industry Notation Standard
The industry came up with a very bad (IMHO) way of expressing it. Even in the professional monitors spec documents, it refers the bit depth as the number of color one pixel can represents. For an 8bit monitor, you can usually read ‘16 million colors’. I have seen software labeling a 16bit image as ‘trillions of color’. Both are correct, but color bit depth is a shorter and more accurate way of defining an image.
To add to the confusion, some systems refer bit depth at the total number of bit allocated per pixel. So an 8bit (per primary) color-coding is referred as (8*3=)24bit, 10bit as 30bit, 12bit as 48bit and so forth. This can be very misleading as you need to also know if there is an alpha channel in the image (see below) without even mentioning the sampling method (422, 444… More about this in another post).
Here is a table of the number of displayable colors depending on the bit depth:
Bit depth per primary color – Levels per primary color – Color resolution
8 256 16,777,216
10 1024 1,073,741,824
12 4096 68,719,476,736
16 65536 281,474,976,710,656
As you can see, an 8bit color depth system can represents 16 million different colors. It would be as true to say that the same system can represents (only) 256 different shades for each primary colors.
Real Life Examples
A blu-Ray disc is encoded in 8bit.
HDCAM-SR is 8bit too unless you are in 444 which is 10bit (in their system).
The new Apple ProRes 4444 codec is 12bit.
The HDMI 1.3 specification defines bit depths of 10-bit, 12-bit & 16-bit per RGB color component.
The ATI FireGL™ V8650 graphic card supports 8-bit, 10-bit & 16-bit per RGB color component.
And most importantly: Most of LCD/plasma/OLED display panels are 8bit. Only very few professional displays are 10bit. NONE of them are 12bit.
In general, it can be cumbersome or even impossible to know the exact bit depth of a given consumer or prosumer equipment. I don’t know why manufactures are so reluctant to include it in their specs. For example: I called Apple the other day, as I wanted to have that information for my MacBook Pro and a Cinema Display I owe. After an hour of waiting on the phone (the tech guy had to ask his supervisor), their answer was ‘we guess it is 8bit’.
Why so many colors?
One could argue that we don’t need trillions of colors to represent an image, as the eye won’t be able to distinguish them all. This is partly true. The eye is actually more receptive to certain color range (green for instance. This comes from our past of hunting in forests or grass fields). Also, our eyes are able to distinguish more or less ‘details’ in different brightness levels. We see more details in the shaded areas than brighter ones.
That said, it doesn’t mean 16bit color bit depth is a waste of digital space. The extra information can be used in post-production for instance. So a colorist can have a wider range available to tweak an image.
This is why it is very important to consider the use of an image before deciding whether to encode it in 8, 10, 12 or 16bit. If the image is captured to be later ‘processed’ (like color corrected, used for a green screen, special effects etc) the higher bit depth the better. But if the image is for broadcasting purposes and so won’t be altered in the future, a 10bit color depth should be sufficient (actually, 8bit is very acceptable).
Also, I am talking, in this blog, only about motion pictures. If you consider the other fields of image processing (medical imaging or astronomy to name just a few), 16bit color depth can be greatly insufficient since they are also greatly interested in what the eye can’t see.
The Alpha channel
There is another information, besides the red, green and blue, an image can carry: the alpha channel.
The alpha channel is transparency information that can be carried alongside an image. It is often referred as a ‘mask’.
Let’s say you create an overlay graphic to be inserted over an image (like a lower third graphic or a title). Not only you want to deliver the image with the proper color information, you also want to give a ‘mask’ that will define, on a pixel per pixel basis, the transparency value.
An image with an N-bit of color depth will be accompany with an equivalent N-bit alpha channel information. So, let say you create a 12bit graphic image, each image’s pixel will have 3*12 bit for each primary color plus 8 bit for it’s transparency level. An image with alpha channel info will be, then, a third larger than one without it.
This is very important as you can see that, if you don’t need it but yet carry the alpha channel information, the final size of your movie file will be unnecessary much bigger. This is an option to look for.
Color bit depth conversion – Banding and Dithering
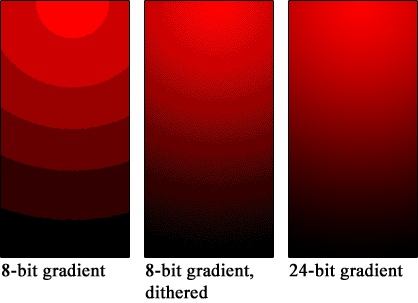
As always, when you consider a processing or transport chain (aka workflow) for your image or video, make sure you will have color bit depth consistency. If not, you will encounter artifacts when converting an image from (downgrading) one bit depth to another. And here comes the problem of banding.
Let say you have a part of a 12bit image defined by 4 different levels of adjacent red (or gray, or any other color group of your choosing). When you convert this image to 10bit, you will divide by 4 the number of available levels. So, in the new quantization, those 4 different levels will be leveled to one. Now, if you have an image that displays a gradient from white to pure red, each section of 4 different red levels will be flattened to just one. So, instead of a smooth transition, you will observe a ‘jump’ from one value to another. A little bit like if you were painting a sunset by numbers (remember those ‘paint by numbers’?). It will look like ‘bands’ of color. That is why that artifact is called ‘color banding’.
One way to address this problem is to randomize the pixels near the edge of such ‘jumps’ in value. This solution is called dithering. Dithering is a process giving the illusion of more available colors by introducing noise to specific areas of an image. For more explanation, I will refer you to the well done Wikipedia page: http://en.wikipedia.org/wiki/Dithering
There are many dithering algorithms available. Some of them are quick, other much more processor intensive. And all of them with various results. But keep in mind that dithering is always a ‘trick’ to improve the appearance of an image.
Be careful at what you are looking
In conclusion, it is always very advisable to ask and check the entire image chain before making an assessment (or start recording). To this date almost all flat panel displays are 8bit. Very few professional ones are 10bit. It is not so important to view a 10bit image on set for instance, but, in order to display an 8bit image from a 10, 12 or 16bit source, the display has to convert it internally. And you don’t know how well it is done. So the artifact you see on screen can very well coming from the screen itself.
As always, an image is as good as the weakest link in the process. And an image is always processed. Just displaying an image requires it to be processed. If you look at an image on your computer, the image will be read from your hard drive, sent to the graphic card (which has it’s own bit depth and dithering process) then to your display panel (which also has its own bit depth and dithering process). Chances are, you are actually looking at less than an 8bit image! Same goes for printing.
So, as always, read the specs (or call the manufacturer) and plan your workflow accordingly.
JD
Short Digital Technique Glossary
A bit is the smallest unit of digital information (or data). It can only be ‘0’ or ‘1’.
A Word is a group of bits carried through your computer or digital device as one pack of information.
If your digital information is coded in 8bit, the smallest value of a word will be 00000000 or 0 in decimal while the highest value would be 11111111 or 255 in decimal.
The simple formula 2^N will give you the number of possible values of a N-bit Word (e.g. A 10bit long Word will have 2^10=1024 different possible values).
WARNING: In Math and your everyday life, you are used to consider ‘1’ as the first value for everything. In the digital world, the first value is ‘0’. It is a very important concept. As an example, I carefully wrote that a N bit long word has 2^N possible values. But since the first possible value is ‘0’, the highest possible value is 2^N-1!! Let’s take our previous example: A 10bit long Word has 2^10=1024 different values. the word ‘0000000000’ will be ‘0’ while the word ‘1111111111’ will be…1023 (or 2^10-1).
The convention is to consider a ‘0’ color intensity to be absent of that color while a 255 (in 8bit) intensity to be saturated of that primary color. So (again in 8bit), 00000000 00000000 000000000 will be pure white, while 11111111 111111111 11111111 will be pure black.
For shorter notations, we often use hexadecimal to represent digital words. Hexadecimal is a 16base numbering system that goes from 0 to F (0,1,2,4,5,6,7,8,9,A,B,C,D,E,F). 0000 is ‘0’ while 1111 if ‘F’. E.g.: pure black in 8bit will be noted FFFFFF which is a much shorter and convenient notation than a suite of 24 ones and zeros. Hexadecimal numbers are often preceded by a ‘#’ or ‘0x’ to note they are of that base system.